Скорость алгоритмов и котики

Давайте посмотрим, как программисты оценивают быстрые и медленные алгоритмы. Поскольку тема максимально занудная, разбираться будем на дурацких примерах с котиками.

Константное время, O(1)

Самый лучший вариант, скорость алгоритма не зависит от количества котиков.

🐾 Пример

Вы — счастливый обладатель N котиков. Каждый котик знает, как его зовут. Если позвать «Клёпа!», то прибежит только он, а остальным N-1 жопкам пофиг.

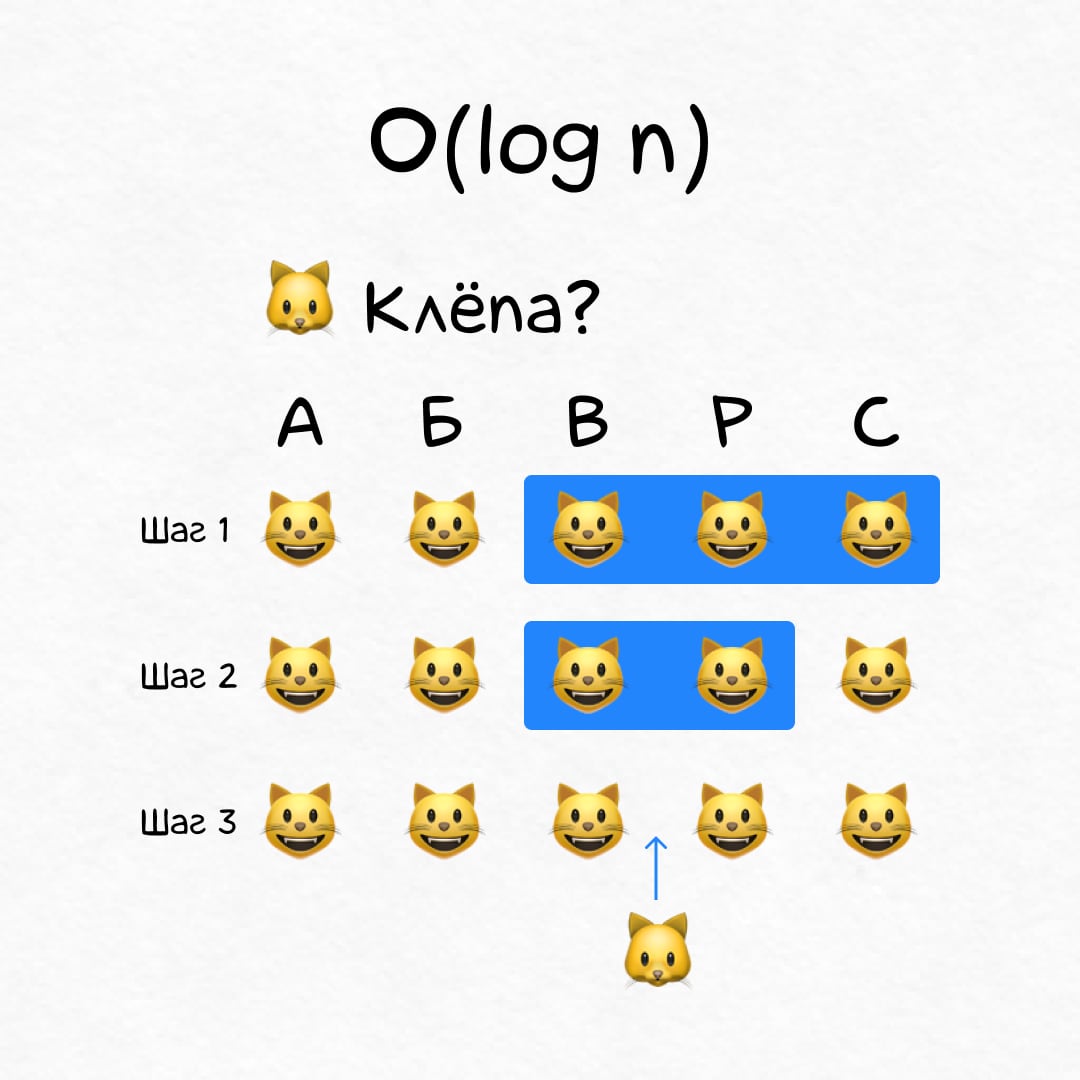
Логарифмическое время, O(log n)

На N котиках алгоритм отрабатывает за log(N) шагов. Это быстро! 1 000 000 котиков → всего 20 операций.

🐾 Пример

Мисочки у котиков расставлены по алфавиту. Когда у вас появляется новый котик, место для его мисочки находится за log(N) шагов.

Линейное время, O(n)

На N котиках алгоритм отрабатывает за N шагов. Это значит, каждый раз приходится перебирать всех кошачьих. Ну такое.

🐾 Пример

Котики взбунтовались и перестали отзываться на клички. Теперь приходится обходить N шубок, чтобы найти нужного.

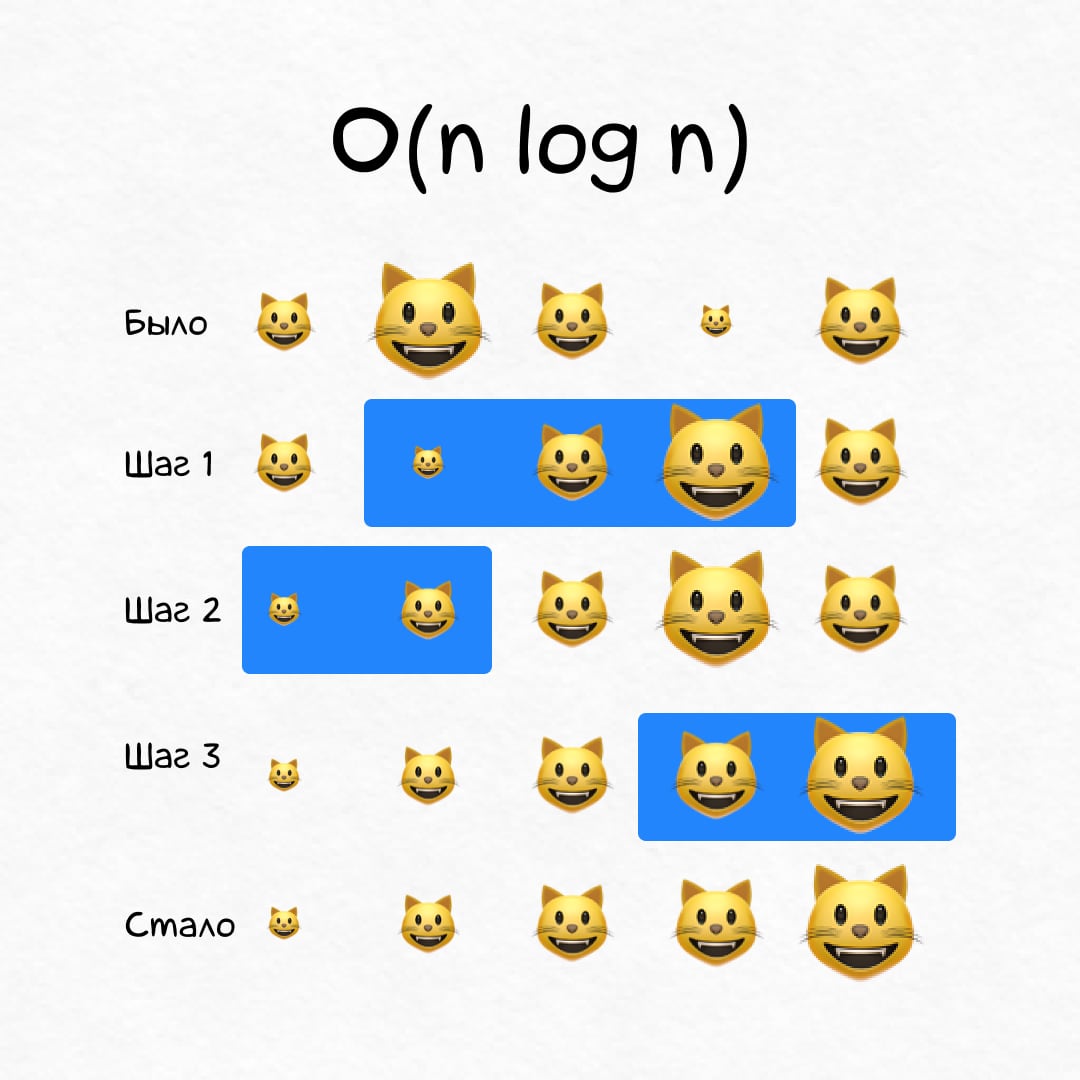
Линейно-логарифмическое время, O(n log n)

На N котиках алгоритм отрабатывает за N × log(N) шагов. Это дольше, чем за линейное время, но ненамного (логарифм N сильно меньше N, помните?).

🐾 Пример

К приходу гостей вы решили рассадить котиков по размеру. Алгоритм quick sort справится с этим за N × log(N) шагов.

На очереди у нас неторопливые полиномиальные котики и совсем улиточки — суперполиномиальные.

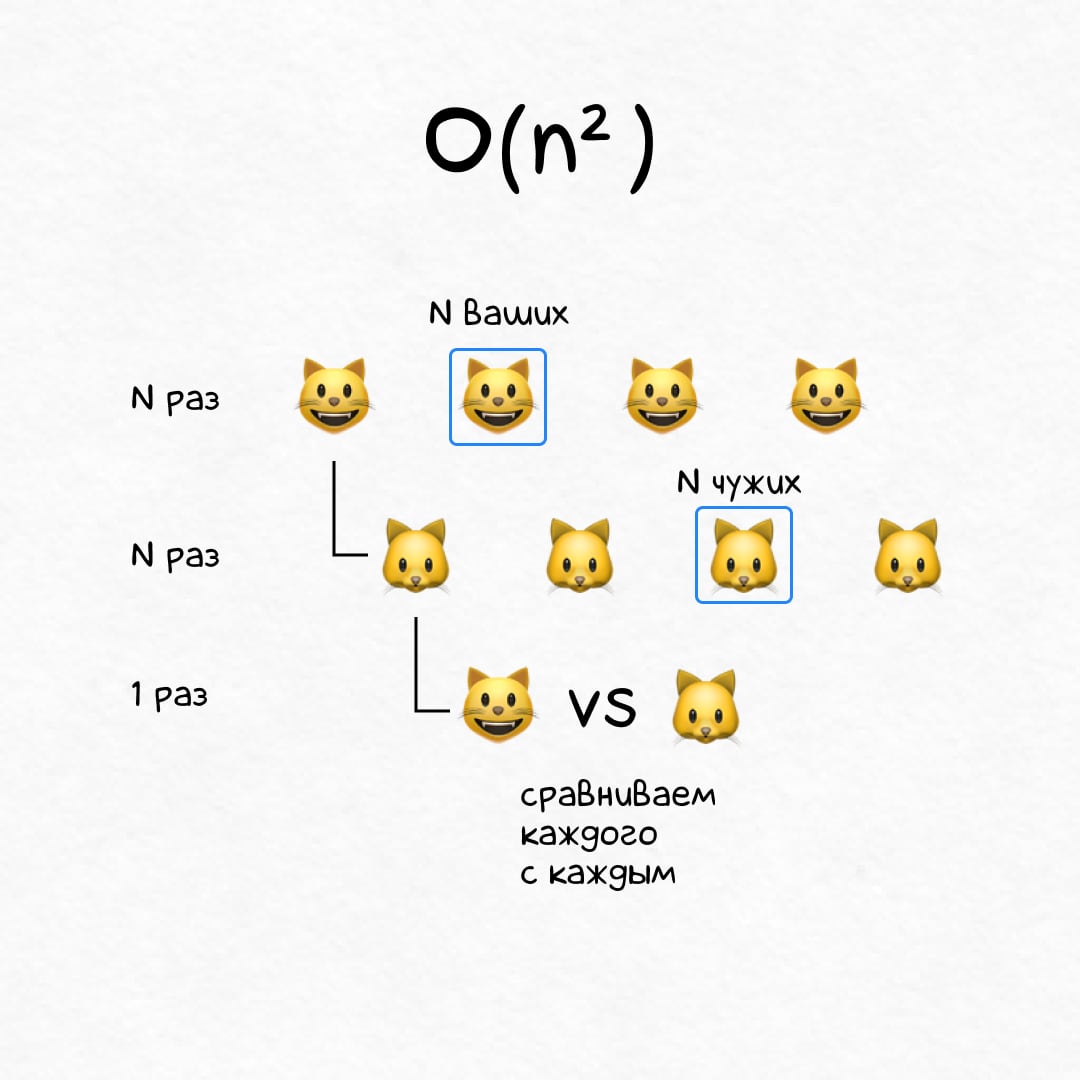
Квадратичное время O(n²)

На N котиках алгоритм отрабатывает за N² шагов. Ме-е-едленно.

🐾 Пример

Конкурент утверждает, что его N котиков более гладкие и довольные, чем ваши. Специальная комиссия попарно сравнит хвостатых и вынесет справедливый вердикт. Понадобится ~ N² сравнений.

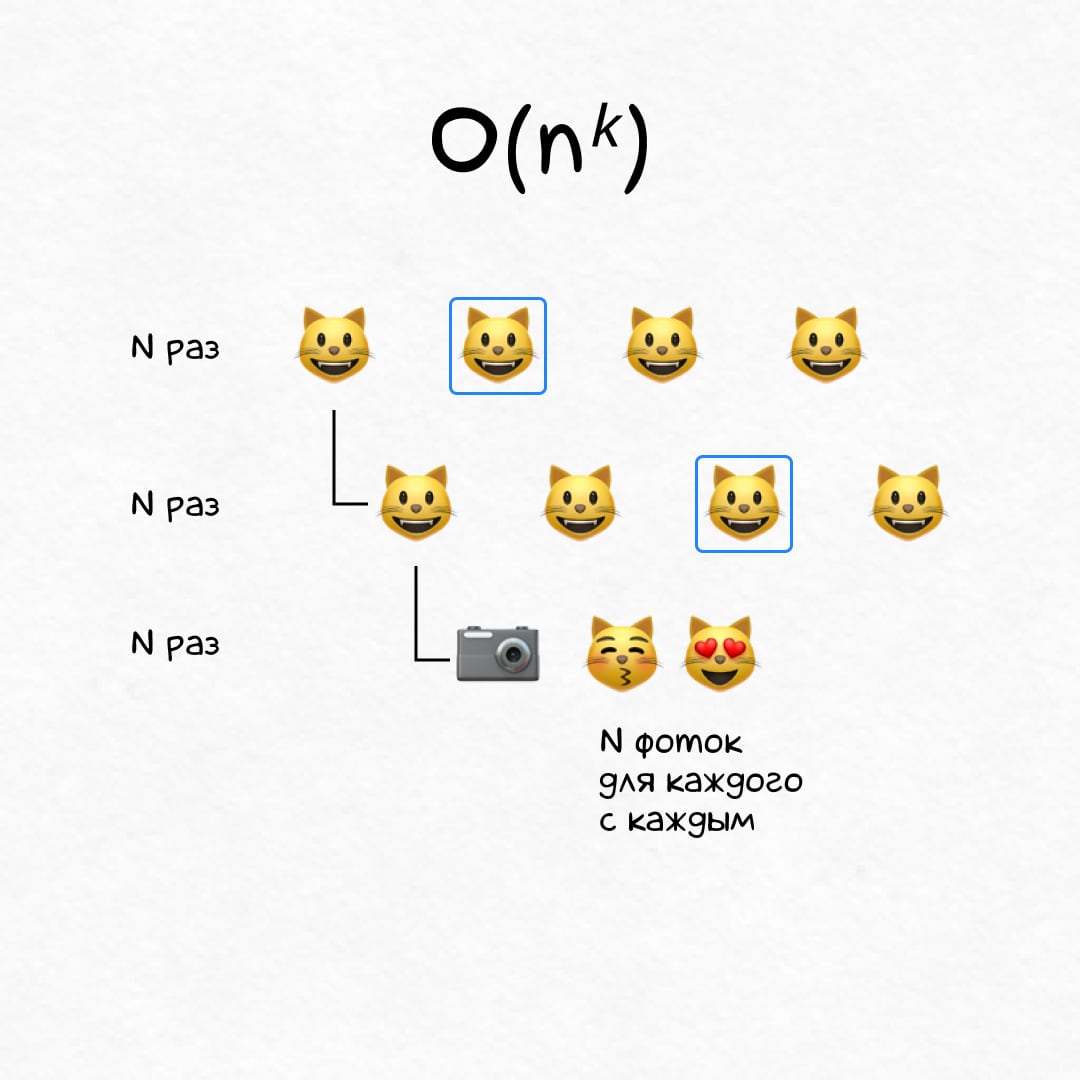
Полиномиальное время, O(nᵏ)

На N котиках алгоритм отрабатывает за N³ шагов, N⁴ шагов, N⁵ шагов, или ещё дольше. Фу таким быть.

🐾 Пример

Фотосессия! Каждого из N котиков надо попарно отфоткать с другими, причем фотограф делает N снимков на каждую пару. N × N × N ≃ N³ шагов.

Хоть полиномиальные алгоритмы и не славятся быстротой, по сравнению с суперполиномиальными они стремительны как Флеш. Из «суперского» у суперполиномиальных только название, увы. Сейчас покажу.

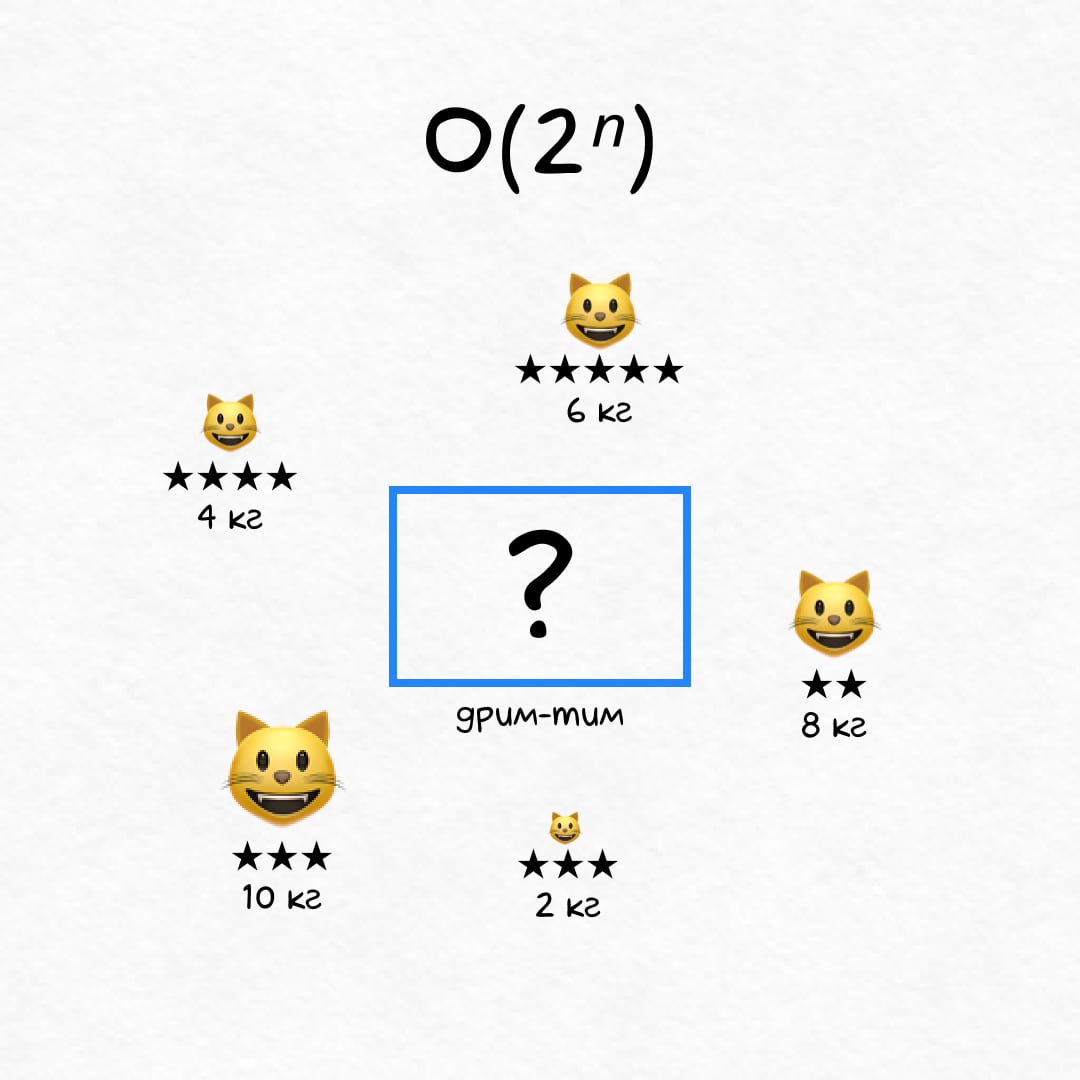
Экспоненциальное время, O(2ⁿ)

На N котиках алгоритм отрабатывает за 2ⁿ шагов. Это долго, вы вряд ли дождетесь.

🐾 Пример

Котики отправляются на выставку. Каждого взвесили и оценили в звездах. Но перевозка рассчитана максимум на X килограмм. Как выбрать самый звездный состав? Ответ потребует 2ⁿ шагов.

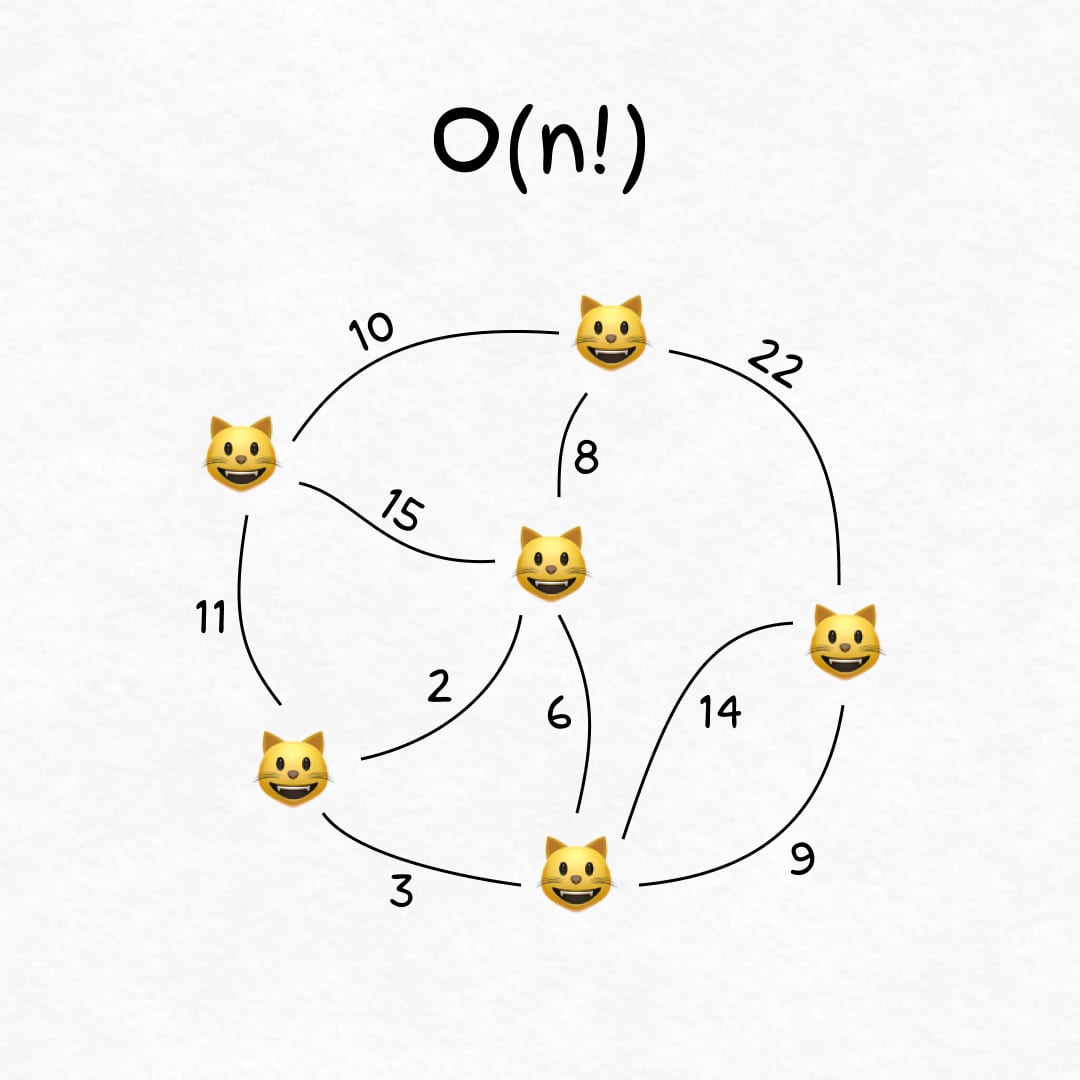
Факториальное время, O(n!)

На N котиках алгоритм отработает за N × (N-1) × (N-2) ×… × 1 шагов. Это жесть! Всего 20 котиков уже дадут нам пару квинтиллионов операций.

🐾 Пример

Котики расселись по квартире. Вам хочется пожамкать каждого, но ходить лень. Какой кратчайший маршрут, чтобы обойти всех шерстяных жопок? Это ~ N! сравнений.

Резюме

Вот какие алгоритмы мы рассмотрели:

• Константные O(1)
• Логарифмические O(log n)
• Линейные O(n)
• Линейно-логарифмические O(n log n)
• Квадратичные O(n²)
• Полиномиальные O(nᵏ)
• Экспоненциальные O(2ⁿ)
• Факториальные O(n!)

Константный алгоритм — всегда лучший вариант, а логарифмический — почти всегда. С линейными и полиномиальными сложнее — тут все зависит от задачи. Где-то стыдно выбирать O(n), а где-то и O(n²) будет большим успехом.

O(2ⁿ) и O(n!) безумно медленные, поэтому на практике вместо них обычно используют неоптимальные, но быстрые алгоритмы.