Как устроен список в Python

Эта заметка посвящена структуре данных номер один в мире — массиву. Если вы еще не гуру алгоритмов и структур данных — гарантирую, что лучше поймете списки в питоне, их преимущества и ограничения. А если и так все знаете — освежите ключевые моменты.

Все знают, как работать со списком в питоне:

>>> guests = ["Френк", "Клер", "Зоя"]
>>> guests[1]
'Клер'

Наверняка вы знаете, что выборка элемента по индексу — guests[idx] — отработает очень быстро даже на списке из миллиона элементов. Более точно, выборка по индексу работает за константное время O(1) — то есть не зависит от количества элементов в списке.

А знаете, за счет чего так быстро работает? Если да — вы в меньшинстве:

Давайте разбираться.

Список = массив?

В основе списка лежит массив. Массив — это набор элементов ① одинакового размера и ② расположенных в памяти подряд друг за другом, без пропусков.

Раз элементы одинаковые и идут подряд, получить элемент массива по индексу несложно — достаточно знать адрес самого первого элемента («головы» массива).

Допустим, голова находится по адресу 0×00001234, а каждый элемент занимает 8 байт. Тогда элемент с индексом idx находится по адресу 0×00001234 + idx*8:

Поскольку операция «получить значение по адресу» выполняется за константное время, то и выборка из массива по индексу выполняется за O(1).

Грубо говоря, список в питоне именно так и устроен. Он хранит указатель на голову массива и количество элементов в массиве. Количество хранится отдельно, чтобы функция len() тоже отрабатывала за O(1), а не считала каждый раз фактическое количество элементов списка.

Все хорошо, но есть пара проблем:

• все элементы массива одного размера, а список умеет хранить разные (true/false, числа, строки разной длины);
• массив имеет фиксированную длину, а в список можно добавить сколько угодно элементов.

Чуть позже посмотрим, как их решить.

Наивный список

Лучший способ освоить структуру данных — реализовать ее с нуля. К сожалению, питон плохо подходит для таких низкоуровненых структур как массив, потому что не дает явно работать с указателями (адресами в памяти).

Но кое-что можно сделать:

class OhMyList:
    def __init__(self):
        self.length = 0
        self.capacity = 8
        self.array = (self.capacity * ctypes.py_object)()

    def append(self, item):
        self.array[self.length] = item
        self.length += 1

    def __len__(self):
        return self.length

    def __getitem__(self, idx):
        return self.array[idx]

Наш самописный список имеет фиксированную вместимость (capacity = 8 элементов) и хранит элементы в массиве array.

Модуль ctypes дает доступ к сишным структурам, на которых построена стандартная библиотека. В даннам случае мы используем его, чтобы создать массив размером в capacity элементов.

Список = массив указателей

Список моментально выбирает элемент по индексу, потому что внутри у него массив. А массив такой быстрый, потому что все элементы у него одинакового размера.

Но при этом в списке элементы могут быть очень разные:

guests = ["Френк", "Клер", "Зоя", True, 42]

Чтобы решить эту задачку, придумали хранить в массиве не сами значения, а указатели на них. Элемент массива — адрес в памяти, а если обратиться по адресу — получишь настоящее значение:

Поскольку указатели фиксированного размера (8 байт на современных 64-битных процессорах), то все прекрасно работает. Да, получается, что вместо одной операции (получить значение из элемента массива) мы делаем две:

1. Получить адрес из элемента массива.
2. Получить значение по адресу.

Но это все еще константное время O(1).

Список = динамический массив

Если в массиве под списком остались свободные места, то метод .append(item) выполнится за константное время — достаточно записать новое значение в свободную ячейку и увеличить счетчик элементов на 1:

def append(self, item):
    self.array[self.length] = item
    self.length += 1

Но что делать, если массив уже заполнен?

Приходится выделять память под новый массив, побольше, и копировать все элементы старого массива в новый:

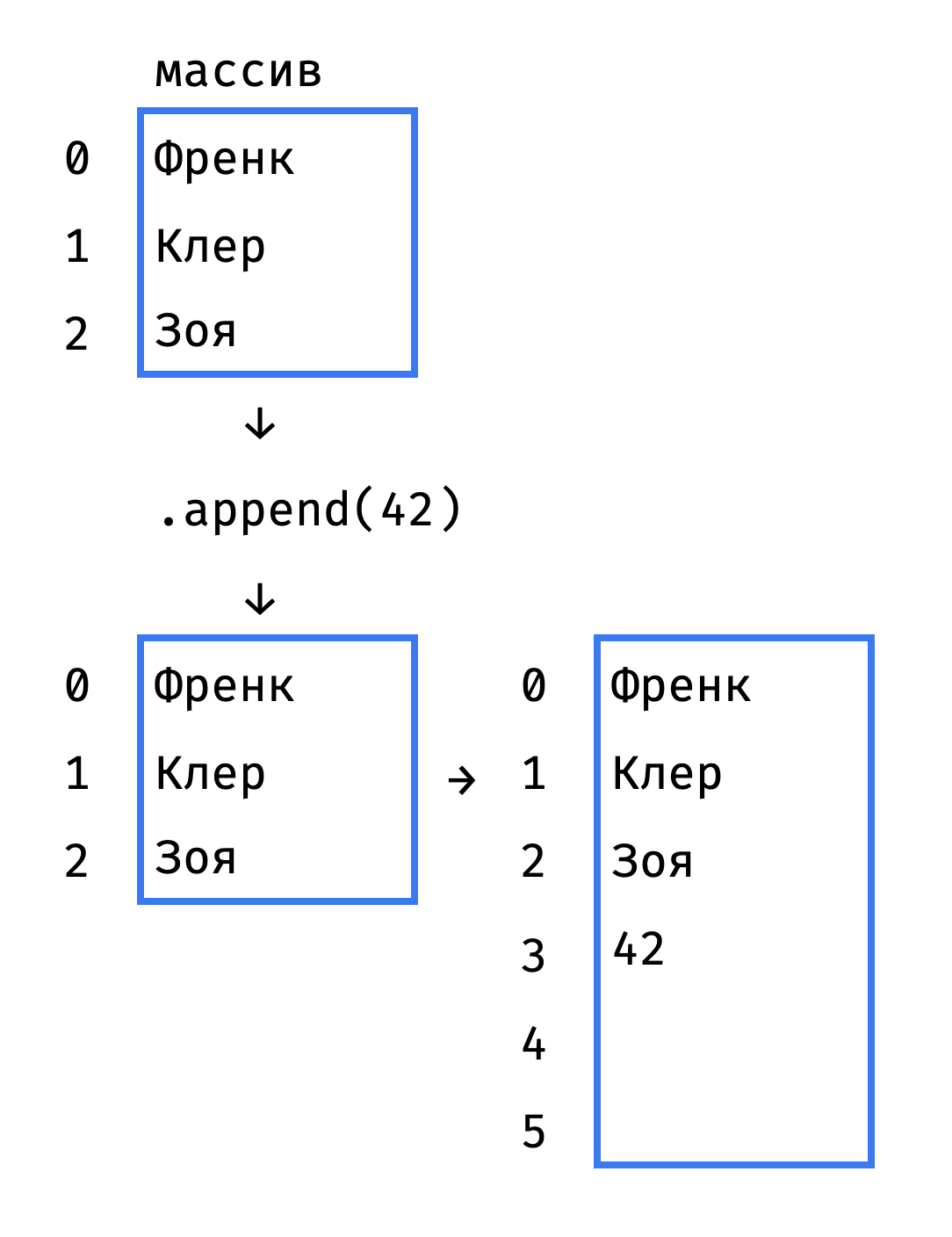
Примерно так:

def append(self, item):
    if self.length == self.capacity:
        self._resize(self.capacity*2)
    self.array[self.length] = item
    self.length += 1

def _resize(self, new_cap):
    new_arr = (new_cap * ctypes.py_object)()
    for idx in range(self.length):
        new_arr[idx] = self.array[idx]
    self.array = new_arr
    self.capacity = new_cap

._resize() — затратная операция, так что новый массив создают с запасом. В примере выше новый массив в два раза больше старого, а в питоне используют более скромный коэффициент — примерно 1.12.

Если удалить из списка больше половины элементов через .pop(), то питон его скукожит — выделит новый массив поменьше и перенесет элементы в него.

Таким образом, список все время жонглирует массивами, чтобы это не приходилось делать нам  ツ

Добавление элемента в конец списка

Выборка из списка по индексу работает за O(1) — с этим разобрались. Метод .append(item) тоже отрабатывает за O(1), пока не приходится расширять массив под списком. Но любое расширение массива — это операция O(n). Так за сколько же в итоге отрабатывает .append()?

Оценивать отдельную операцию вставки было бы неправильно — как мы выяснили, она иногда выполняется за O(1), а иногда и за O(n). Поэтому используют амортизационный анализ — оценивают общее время, которое займет последовательность из K операций, затем делят его на K и получают амортизированное время одной операции.

Так вот. Не вдаваясь в подробности скажу, что амортизированное время для .append(item) получается константным — O(1). Так что вставка в конец списка работает очень быстро.

1 + 2 + 4 + ... log(n) = 
= 2**log(n) * 2 - 1 =
= 2n - 1

Получается, у списка есть такие гарантированно быстрые операции:

# O(1)
lst[idx]

# O(1)
len(lst)

# амортизированное O(1)
lst.append(item)
lst.pop()

Внутренности списка

Алгоритм обсудили, посмотрим теперь на реализацию.

Основные структуры данных Python реализованы на C, и список не исключение. Вот (радикально упрощенная) структура списка из исходников Python (см. listobject.h, listobject.c):

// Структура списка.
typedef struct {
    // длина (количество элементов) списка
    Py_ssize_t ob_size;

    // указатели на элементы списка; list[0] = ob_item[0], итд
    PyObject** ob_item;

    // вместимость списка
    // 0 <= ob_size <= allocated
    // len(list) == ob_size
    Py_ssize_t allocated;
} PyListObject;

Как и наша наивная реализация, настоящий список содержит длину (ob_size), вместимость (allocated) и массив элементов (ob_item).

Конструктор списка:

// Создает новый список.
PyObject* PyList_New(Py_ssize_t size) {
    PyListObject *op;

    // выделяем память под сам список (без учета элементов списка)
    op = PyObject_GC_New(PyListObject, &PyList_Type);

    // выделяем память под элементы списка
    op->ob_item = (PyObject**) PyMem_Calloc(size, sizeof(PyObject*));

    return (PyObject*) op;
}

Реализация len() просто возвращает значение поля ob_size:

// Возвращает длину списка.
static inline Py_ssize_t PyList_GET_SIZE(PyListObject* self) {
    return list->ob_size;
}

Выборка и запись элемента списка по индексу тоже реализуются тривиально:

// Возвращает элемент списка по индексу.
static inline PyObject* PyList_GET_ITEM(PyObject* op, Py_ssize_t index) {
    PyListObject* list = _PyList_CAST(op);
    return list->ob_item[index];
}

// Устанавливает элемент списка по индексу.
static inline void PyList_SET_ITEM(PyObject* op, Py_ssize_t index, PyObject* value) {
    PyListObject* list = _PyList_CAST(op);
    list->ob_item[index] = value;
}

А вот и добавление элемента:

// Добавляет элемент в конец списка.
static PyObject* list_append(PyListObject* self, PyObject* object) {
    // длина списка
    Py_ssize_t len = PyList_GET_SIZE(self);

    // вместимость списка
    Py_ssize_t allocated = self->allocated;

    // если в списке есть свободное место (length < capacity),
    // добавляем новый элемент без расширения списка
    if (allocated > len) {
        PyList_SET_ITEM(self, len, newitem);
        Py_SET_SIZE(self, len + 1);
        return 0;
    }

    // иначе, расширяем список
    list_resize(self, len + 1);
    // затем добавляем новый элемент
    PyList_SET_ITEM(self, len, newitem);
    return 0;
}

Как мы обсуждали, иногда добавление нового элемента приводит к расширению списка:

// Расширяет список, тем самым увеличивая его вместимость.
static int list_resize(PyListObject* self, Py_ssize_t newsize) {
    // вместимость списка
    Py_ssize_t allocated = self->allocated;

    // считаем новую вместимость
    // последовательность роста: 0, 4, 8, 16, 24, 32, 40, 52, 64, 76, ...
    size_t new_allocated = ((size_t)newsize + (newsize >> 3) + 6) & ~(size_t)3;

    // выделяем память под расширенный список
    // и копируем элементы списка в новый блок памяти, если необходимо
    size_t num_allocated_bytes = new_allocated * sizeof(PyObject*);
    PyObject** items = (PyObject**)PyMem_Realloc(self->ob_item, num_allocated_bytes);
    self->ob_item = items;

    // устанавливаем новую длину и вместимость списка
    Py_SET_SIZE(self, newsize);
    self->allocated = new_allocated;
    return 0;
}

Вот и все!

Итоги

Как мы выяснили, у списка работают за O(1):

• выборка по индексу lst[idx]
• запрос длины len(lst)
• добавление элемента в конец списка .append(item)
• удаление элемента из конца списка .pop()

Остальные операции — «медленные»:

• Вставка и удаление из произвольной позиции — .insert(idx, item) и .pop(idx) — работают за линейное время O(n), потому что сдвигают все элементы после целевого.
• Поиск и удаление элемента по значению — item in lst, .index(item) и .remove(item) — работают за линейное время O(n), потому что перебирают все элементы.
• Выборка среза из k элементов — lst[from:to] — работает за O(k).

Значит ли это, что «медленные» операции нельзя использовать? Конечно, нет. Если у вас список из 1000 элементов, разница между O(1) и O(n) для единичной операции незаметна.

С другой стороны, если вы миллион раз выполняете «медленную» операцию на списке из 1000 элементов — это уже заметно. Или если список из миллиона элементов — тоже.

Поэтому полезно знать, что у списка работает за константное время, а что за линейное — чтобы осознанно принимать решение в конкретной ситуации.